PUBLICIDADE
Hoje em dia é comum a introdução ao cálculo de limites e derivação na terceira série do ensino médio. Essas ferramentas matemáticas são de extrema utilidade para análise do comportamento de funções e construção de gráficos. É bom lembrar que, ao serem trabalhados esses conceitos no ensino médio, trabalhamos somente com a ideia intuitiva, não explorando definições que, provavelmente, causariam muita confusão e distanciariam do objetivo dessas ferramentas nesta etapa da vida escolar.
Porém, no estudo dos limites de uma função há casos em que nos deparamos com indeterminações do tipo:
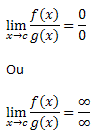
Nesses casos recorremos a diversos casos de fatoração para tentarmos driblar a indeterminação, como por exemplo:
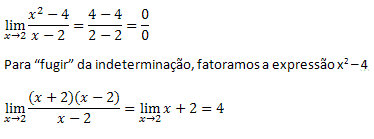
No entanto há situações em que não é possível utilizar nenhum desses artifícios. Para esses casos utilizamos as regras de L´Hopital, que podem ser muito bem trabalhadas no ensino médio, sempre com a finalidade de facilitar a intepretação do comportamento das funções e a construção de gráficos.
A primeira regra de L´Hopital diz que:

A segunda regra diz que:
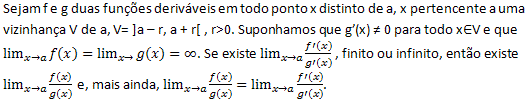
Conhecendo as duas propriedades, fica mais fácil o cálculo dos limites que aparecem nas indeterminações citadas anteriormente. Deixe bem claro aos alunos que essas propriedades só podem ser utilizadas se as hipóteses forem satisfeitas.
Exemplo:
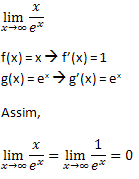
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola





