PUBLICIDADE
Ao colocarmos um bloco de massa qualquer em um plano inclinado, o bloco fica sujeito a duas forças: seu peso ![]() , em virtude da atração da Terra, vertical para baixo; e a força normal
, em virtude da atração da Terra, vertical para baixo; e a força normal ![]() , exercida pelo plano inclinado, no caso. Iremos notar que a força peso
, exercida pelo plano inclinado, no caso. Iremos notar que a força peso ![]() será decomposta em duas componentes, uma na direção y e outra na direção x, que chamamos de Py e Px. Na maioria dos nossos estudos fazemos uso da componente Px.
será decomposta em duas componentes, uma na direção y e outra na direção x, que chamamos de Py e Px. Na maioria dos nossos estudos fazemos uso da componente Px.
O experimento aqui retratado é de baixo custo e tem por finalidade determinar o valor da componente Px, de forma com que o próprio estudante seja o agente do conhecimento dessa componente, pois, em muitos casos, os alunos apresentam dificuldades em “enxergá-la”.
Material a ser utilizado
- um carrinho em miniatura de peso conhecido, que se movimente livremente
- uma tábua pequena e plana
- um transferidor
- uma mola de constante elástica k conhecida
- um prego fino pequeno
Com esse material você pode determinar o módulo (Px) da componente tangencial do peso do carrinho e verificar a validade da expressão Px = P.sen θ. Para isso, prenda o carrinho à mola e esta ao prego fixado à extremidade superior da tábua. Em seguida, incline-a.
Observe que, à medida que o ângulo de inclinação aumenta, o alongamento x da mola aumenta, mostrando que o módulo da força exercida sobre a mola, componente tangencial do peso (![]() ), aumenta. Vejamos a ilustração abaixo:
), aumenta. Vejamos a ilustração abaixo:
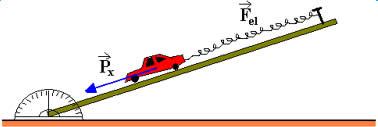
Escolha alguns ângulos de inclinação para a tábua, como, por exemplo, 30°, 37°, 45°, 53, 60°, etc. Para cada um dos ângulos de inclinação, sugerimos o seguinte procedimento:
- calcule o módulo de Px pela equação Px = P.sen θ
- aplicando a lei de Hooke, F = kx, calcule o módulo da força exercida pela mola.
Verifique se o módulo de ![]() é igual ao módulo calculado de
é igual ao módulo calculado de![]() .
.
Por Domiciano Marques
Graduado em Física
Equipe Brasil Escola





