PUBLICIDADE
Esta atividade tem dois objetivos: construir pelo menos duas elipses de excentricidade diferentes e dar uma ideia mais próxima da forma da órbita elíptica descrita pelos planetas.
Ao estudarmos geometria, vimos que elipse é o lugar geométrico dos pontos de um plano cuja soma das distâncias a dois pontos fixos (ou seja, o foco) desse plano é constante. Portanto, para construir graficamente uma elipse é preciso estabelecer um procedimento em que sejam fixados esses dois pontos e um dispositivo que possibilite o traçado da curva, mantendo a condição da soma constante das distâncias a esses pontos. A seguir temos a descrição desse procedimento:
- fixe sobre uma mesa ou base de madeira dois alfinetes separados por uma distância d;
- faça um anel de barbante fino cujo perímetro, p, seja maior do que o dobro da distância d (sugestão: p = 30 cm, d = 12 cm);
- envolva os dois alfinetes com o anel e, com uma caneta ou lápis, abra ao máximo o anel, mantendo-o distendido. Em seguida, faça a caneta deslizar sobre o papel desenhando a elipse.
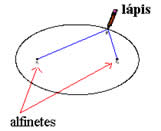
- agora reduza a distância d (sugestão d = 1 cm) e construa uma nova elipse.
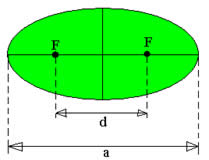
Assim você terá construído duas elipses de excentricidades diferentes. A excentricidade, e, da elipse é dada pela razão e = d/a em que a é o comprimento do seu eixo maior. Vejamos a figura abaixo:
Com a finalidade de completar essa atividade, você pode fazer alguns questionamentos aos alunos:
1) Qual a excentricidade das elipses que o aluno construiu?
2) Qual elipse se aproxima mais da órbita de um planeta em torno do Sol? Ela é mais ou menos circular do que a órbita real?
Por Domiciano Marques
Graduado em Física
Equipe Brasil Escola





