PUBLICIDADE
Quando nós, professores de matemática, vamos introduzir o conteúdo de circunferência, círculo ou ciclo trigonométrico nos deparamos com a curiosidade de nossos alunos a respeito da obtenção do valor de π. Imediatamente recorremos ao método de tomar qualquer circunferência, medir seu perímetro e dividi-lo pelo comprimento do diâmetro, obtendo sempre um valor próximo a 3,14 para qualquer que seja a circunferência tomada. A fim de tornar a aula mais atrativa e dinâmica, podemos propor essa atividade para ser feita em sala, estimulando os alunos a levarem de casa CDs, discos de vinil e outros objetos circulares, permitindo que eles mesmos obtenham o valor aproximado de π, fazendo uma tabela com os valores encontrados para os diversos objetos que trouxeram. Mas, afinal, existe somente essa forma de se obter um valor aproximado de π?
Bem, Georges Louis Leclerc, conde de Buffon (1707-1788), e Pierre Simon Laplace (1749-1827) propuseram uma maneira distinta para se obter praticamente o valor de π. Essa forma diferente é bastante lúdica e pode ser feita em sala de aula.
Seguem os passos do processo:
Trace um quadrado de lado 2r (r deve ser bem grande em relação ao tamanho de uma moeda) e inscreva nesse quadrado um círculo. Lançando, ao acaso, uma moeda sobre a figura, anota-se o número m de vezes que ela cairá dentro do círculo e o número n de vezes que ela cairá dentro do quadrado, mas fora do círculo. A razão m/(m + n) é, aproximadamente, igual à razão das áreas do círculo e do quadrado:
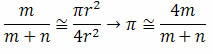
É obvio que quanto maior o número de lançamentos melhor será a aproximação do valor real de π.
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola





