PUBLICIDADE
No estudo dos produtos notáveis, ao trabalhar com o trinômio do quadrado perfeito, mostramos aos alunos como desenvolvê-lo utilizando uma regra prática e de simples compreensão. Geralmente, a maioria compreende o dispositivo prático e como obter a forma desenvolvida de maneira correta. O problema surge quando a turma depara-se com o problema inverso: fatorar o produto que está desenvolvido e, pior ainda, completar a expressão para obter um trinômio quadrado perfeito. A utilização do dispositivo prático para obter a forma fatorada é o recurso mais utilizado, porém de difícil entendimento. Vejamos como isso é feito.
Primeiro, o desenvolvimento do produto notável:
(a + b)2 = (quadrado do primeiro termo) + (o dobro do produto do primeiro pelo segundo termo) + (quadrado do segundo termo)
(x + 3)2 = x2 + 2*x*3 + 32 = x2 + 6x + 9
Essa etapa, como foi dito, é de simples compreensão. Agora, vamos analisar o processo de completar quadrados utilizando esse método prático.
Complete a expressão abaixo para obter um trinômio do quadrado perfeito.
x2 + 12x = 64
O objetivo é obter uma expressão do lado esquerdo da igualdade que apresente a seguinte forma (x + __)2, utilizando o método de completar quadrados. O aluno até pode conseguir compreender o método e colocá-lo em prática, mas ficará se perguntando: “Por que se diz completar quadrados?”. Não há como visualizar o motivo pelo qual o processo recebe essa denominação. O que há de sugestão é representar geometricamente o procedimento para que o aluno compreenda a denominação e como se proceder para obter a solução do problema, além de ser outra forma de se chegar à resposta correta.
Observe como podemos completar quadrados na expressão x2 + 12x = 64.
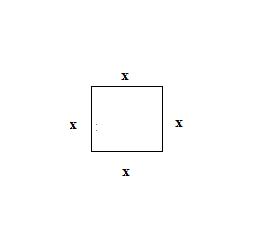
1º: Construa um quadrado de lados x.
A área do quadrado representa o termo x2.
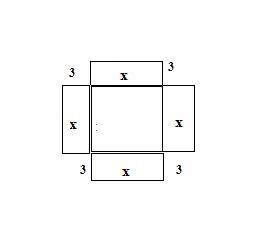
2º: Para representar o termo 12x construa quatro retângulos de lados 3 e x, como mostra a figura.
3º: Questione o que deve ser feito para que a figura obtida se transforme em um quadrado.
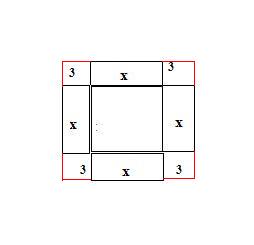
4º: Complete a figura com quatro quadrados de lados com medida 3, como mostra a figura.
5º: A área do quadrado maior representa o método de completar quadrados.
x2 + 4*3x + 4*9 = x2 + 12x + 36 = (x + 6)2
Assim, a expressão resultante seria:
x2 + 12x + 36 = 64 + 36 ou x2 + 12x + 36 = 100
Explique que o motivo de se adicionar 36 do lado direito da igualdade deve-se ao fato de que tudo o que se faz de um lado deve ser feito do outro para manter a igualdade satisfeita, “equilibrada”.
Dessa forma o aluno compreende o motivo de o processo ser denominado por “completar quadrados” e visualiza a figura que precisou ser completada para se obter um quadrado.
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola