PUBLICIDADE
Os conceitos de menor múltiplo comum e maior denominador comum são introduzidos após o aluno conhecer a ideia de múltiplos e divisores. As maneiras pelas quais podemos obter o MMC e MDC podem ser as mais variadas, mas comumente encontramos esses valores realizando a fatoração por números primos ou escrevendo a sequência dos múltiplos e divisores dos números. Há uma forma de se obter o MMC e o MDC sem realização de cálculos, usando apenas uma contagem simples. Podemos denominar de uma interpretação geométrica desses valores, uma maneira mais lúdica de obtê-los.
Vejamos o método para obtenção do MMC e do MDC produzido pelo professor Marcelo Polezzi.
Construa um retângulo de lados medindo a e b, sendo a e b números inteiros, dividido em quadradinhos unitários. Trance uma das diagonais do retângulo e marque os pontos que são vértices de algum quadradinho unitário. Faça a contagem de quantas partes esses pontos dividem a diagonal. O número obtido é o MDC(a, b). Trace linhas verticais e horizontais passando por cada ponto marcado, unindo os lados opostos do retângulo. O número de quadradinhos unitários existentes em qualquer um dos retângulos determinado é o MMC(a, b)
Vamos fazer um exemplo para o MMC(5, 10) e MDC(5, 10).
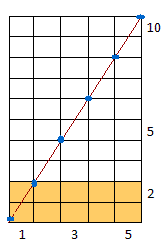
Observe que a diagonal do retângulo passa pelos vértices de 6 quadradinhos unitários e consequentemente fica dividida em 5 partes iguais, portanto, MDC(5, 10) = 5. Perceba também que a diagonal divide o retângulo maior em 5 retângulos menores e cada um deles possui, igualmente, 10 quadradinhos unitários (parte amarela), concluindo que MMC(5, 10) = 10.
Dessa forma, para o MDC e o MMC de 8 e 12, teremos:
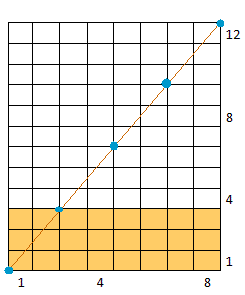
A diagonal do retângulo está dividida em 4 partes, assim, MDC(8, 12) = 4. Observe que a diagonal divide o retângulo maior em quatro retângulos menores, cada um contendo 28 quadradinhos unitários, portanto, MMC(8, 12) = 24.
É interessante notar que trabalhando o conteúdo de múltiplos e divisores, menor múltiplo comum e maior divisor comum com essa abordagem também fixamos conceitos geométricos como a área de um retângulo, vértices e diagonais.
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola





