PUBLICIDADE
As demonstrações de fórmulas e teoremas nas aulas de matemática são fundamentais para que nossos estudantes entendam e passem a gostar da disciplina, compreendendo o caráter investigativo e criativo do matemático ao obter o resultado procurado. Dessa forma, veremos uma demonstração para o método de verificação da condição de alinhamento de três pontos distintos no plano cartesiano. Percebemos que na maioria dos livros didáticos não há essa demonstração que, de certa forma, é simples, bastando conhecer os conceitos de semelhança de triângulos e segmentos proporcionais.
Considere três pontos distintos do plano: A(xA, yA), B(xB, yB) e C(xC, yC). Suponhamos que esses pontos estejam alinhados. Assim, teremos a seguinte representação gráfica.
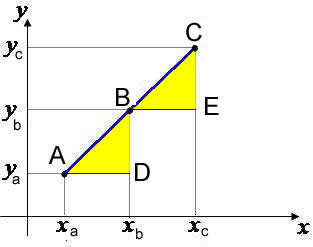
Verifique que os triângulos ABD e BCE são semelhantes. Assim, obtemos:
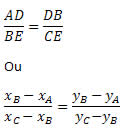
Aplicando a propriedade das proporções, teremos:
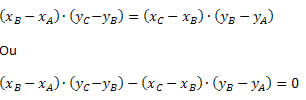
Desenvolvendo os produtos, obtemos:
![]()
Reorganizando os termos, teremos:
![]()
Vamos verificar que a expressão (I) é equivalente à:
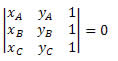
Desenvolvendo o determinante, obtemos:
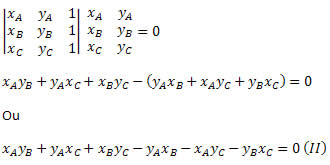
Constatamos que as duas expressões são equivalentes. Assim, podemos afirmar que A(xA, yA), B(xB, yB) e C(xC, yC) estão alinhados se:
.jpg)
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola





