Sabemos da importância da demonstração de fórmulas nas aulas de matemática para que o aluno perceba como se trabalha o conhecimento matemático e para mostrar que as fórmulas não se tratam de invenções do acaso. Pensando dessa forma, veremos como demonstrar a fórmula da área de um triângulo equilátero.
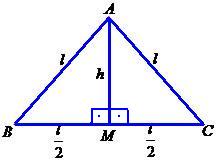
Considere um triângulo equilátero ABC de lado l, como mostra a figura.
A área de um triângulo qualquer é dada por:
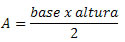
No caso do triângulo equilátero não conhecemos o valor da altura, somente dos lados, porém, é fácil determinar a altura em função da medida do lado. Para isso, basta lembrar que a altura é, também, mediana, mediatriz e bissetriz do triângulo equilátero. Assim, teremos a figura abaixo.
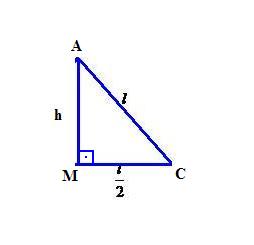
O triângulo AMC é retângulo em M, pois AM é a altura do triângulo. Sabemos que M é o ponto médio do lado BC. Dessa forma, podemos utilizar o teorema de Pitágoras obtendo a seguinte igualdade:
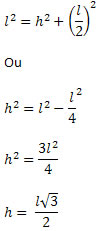
Obtemos, assim, a altura do triângulo equilátero em função da medida do lado.
Como a base do triângulo equilátero é l, sua área será dada por:
Não pare agora... Tem mais depois da publicidade ;)
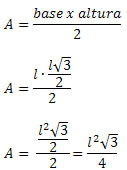
Também podemos obter a área do triângulo equilátero usando as relações trigonométricas no triângulo retângulo. Veja:
Sabemos que num triângulo equilátero cada ângulo interno mede 60o. Como a altura do triângulo equilátero é também bissetriz, teremos:
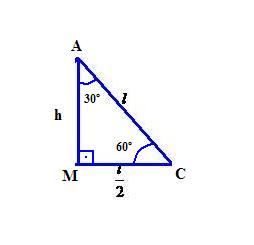
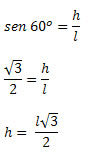
Encontrada a altura em função do lado, substituímos na fórmula da área de um triângulo qualquer e obtemos a sentença matemática que determina a área de um triângulo equilátero.
Note que é uma demonstração simples, de fácil compreensão e que pode ser feita de duas formas, envolvendo relações métricas e trigonométricas no triângulo retângulo. É fundamental para o aluno ter consciência de que o conhecimento matemático é produzido utilizando o que previamente já havia sido constatado e que tudo tem uma sequência lógica, com justificativas e argumentações que seguem normas e padrões científicos.
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola