PUBLICIDADE
Demonstrar fórmulas e teoremas é fundamental para que o aluno compreenda que a matemática é uma ciência (assim como outras) que apresenta seus resultados mediante a observação e comprovação dos fatos, utilizando o conhecimento prévio e conceitos já definidos. Além disso, as demonstrações mostram aos educandos o pensamento matemático, a criatividade e a investigação de quem se dedicou ao estudo de tal fato, conseguindo provar as relações existente em cada caso. Serve também para mudar a visão de que o aluno precisa somente saber aplicar a fórmula, contribuindo para que ele passe a gostar de matemática e tenha interesse em adquirir conhecimento nessa área.
Veremos uma demonstração da fórmula para cos (a – b) utilizando o conceito de distância entre dois pontos.
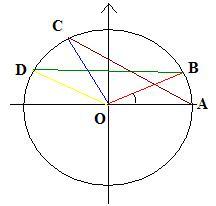
Considere quatro pontos pertencentes à circunferência trigonométrica como mostra a figura a seguir:
Temos que:
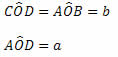
Como sabemos, a circunferência trigonométrica apresenta raio unitário. Assim, os pontos apresentam coordenadas: A(1, 0); B(Xb, Yb); C(Xc, Yc) e D(Xd, Yd). Note que Xb = cos b, Yb = sen b, Xc = cos (a – b), Yc = sen (a – b), Xd = cos a e Yd = sen a.
Observe que a distância entre os pontos B e D é igual à distância entre C e A. Obtemos essa igualdade da congruência entre os triângulos BOD e AOC, pelo caso Lado – Ângulo – Lado.
Utilizando a fórmula da distância entre dois pontos, obtemos:
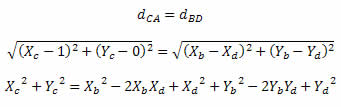
Substituindo os valores das coordenadas na igualdade acima, obtemos:
![]()
Como
![]()
Obtemos
![]()
Ou
![]()
Como queríamos demonstrar.
Veja que se trata de uma demonstração simples, utilizando a distância entre dois pontos, que nada mais é que o Teorema de Pitágoras e conceitos básicos de trigonometria no ciclo. Dessa forma, o aluno não fica com a ideia de que o modelo matemático “caiu do céu”, não havendo explicação para tal fato, aceitando a veracidade da fórmula como uma verdade absoluta, imposta.
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola