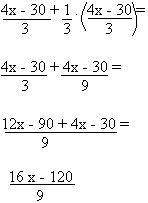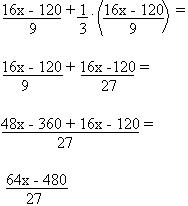PUBLICIDADE
Ao final dos conteúdos é interessante propor alguns desafios que relacionam o conteúdo aprendido, pois além dos alunos colocarem em prática os conhecimentos adquiridos eles terão a oportunidade de desenvolver a capacidade de resolver problemas matemáticos.
O estudo de equação está diretamente ligado com problemas matemáticos, assim os desafios que envolvem equações são em sua maioria situações problemas, veja alguns desafios que podem ser aplicados nas aulas de matemática e suas respectivas soluções.
Problema: As três árvores
Num sítio havia 3 árvores carregadas de mangas. Ana e Marta colheram certo número de mangas da primeira árvore, mas jogaram 6 fora, pois estavam estragadas. Da segunda árvore colheram um número de mangas equivalente a das que havia sobrado, mas voltaram a jogar 2 fora. Da terceira árvore, colheram
do total que tinham até então e,
sem jogar nenhuma fora, apanharam ainda dessa árvore mais de quantas mangas
tinham até aquele momento. Ficaram assim com o dobro do número de mangas que tinham colhido da primeira árvore. Diga-me, quantas mangas Ana e Marta colheram da primeira árvore?
Resolução:
Devemos equacionar as informações.
• Ana e Marta colheram certo número de mangas da primeira árvore: x
• Jogaram fora 6: x – 6
• Da segunda árvore, colheram 1 das que restaram: x – 6 + x – 6
3 3
• Jogaram fora 2: ![]()
• Da terceira árvore, colheram do total que tinham até então:
• E depois mais 1/3 de quantas tinham colhido até aquele momento:
• Ficaram com o dobro das mangas colhidas da primeira árvore: 64x – 480 = 2x
27
Resolvendo a equação encontrada temos:
64x – 480 = 2x
27
64x – 480 = 54x
64x – 54x = 480
10x = 480
x = 480 : 10
x = 48
Resposta: Da 1º árvore foram colhidas 48 mangas.
Problema: quantos anos ela tem?
Quantos anos têm Ana e Marta, se a soma das idades mais a diferença entre elas mais o seu produto é igual a 100 anos, e Ana é mais velha do que Marta?
Resolução:
Iremos estipular: a idade de Ana como sendo X e a idade de Marta como sendo Y, portanto, equacionamos as informações dadas no problema.
(x + y) – (x – y) + xy = 100
Vamos isolar y, ou seja, deixar o valor de y em função de x>
x + y + x – y + xy = 100
2x + xy = 100
x (2 + y) = 100
2 + y = 100
x
y = 100 - 2
x
Como x e y representam idades, os seus valores serão números inteiros, portanto observando a equação encontrada x é um divisor de 100, então x poderá ser:
1, 2, 4, 5, 10, 20, 25, 50, 100.
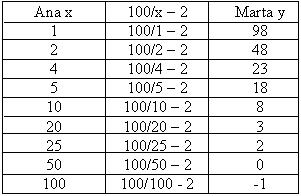
Substituindo esses valores de x na equação iremos obter para cada valor acima um valor pra y, veja:
Observando os valores encontrados e algumas informações dadas no enunciado, podemos obter a seguinte resposta:
Resposta: como o problema diz que Ana é mais velha que Marta, Ana e Marta podem ter, respectivamente, 10 anos e 8 anos, 20 anos e 3 anos ou 25 anos e 2 anos.
Problema: cento de aves
Se um galo vale 5 yuan, uma galinha 3 e três frangos valem 1, quantos de cada um podem comprar com 100 yuan, de modo que sejam 100 aves ao todo e pelo menos 4 galos?
Resolução:
Devemos representar cada ave por uma letra para facilitar a montagem da equação. O número de galos será representado por x, o número de galinhas por y e o número de frangos por z.
x + y + z = 100
5x + 3y + 1/3z = 100
Na segunda equação encontrada podemos colocar z em função de x e y:
1/3z = 100 – 5x – 3y
z = 3 (100 – 5x – 3y)
z = 300 – 15x – 9y
Substituindo o valor de z encontrado na primeira equação, temos:
x + y + 300 – 15x – 9y = 100
-14x – 8y = 100 – 300
-14x – 8y = -200 dividindo a equação por -2 temos:
7x + 4y = 100
Isolamos y:
4y = 100 – 7x
y = 100 – 7x
4
y = 100 – 7x
4 4
y = 25 – 7 . x/4
Como os valor que x e y representam quantidades, essas quantidades são representadas por números naturais, assim os valores que x irá assumir serão múltiplos de 4. Portanto, x poderá assumir valores iguais a:
0, 4, 8, 12, 16, 20. Substituindo os mesmo na equação 300 – 15x – 9y, teremos valores para y, veja:
Excluímos alguns resultados, como o que x é igual a zero e os resultados que constam y iguais a valores negativos. Com as informações do problema, chegamos a uma conclusão:
Resposta: Como são 100 aves ao todo e pelo menos 4 galos, concluímos que com 100 yuan é possível comprar:
- 4 galos, 18 galinhas e 78 frangos.
- 8 galos, 11 galinhas e 81 frangos.
- 12 galos, 4 galinhas e 84 frangos.
Por Danielle de Miranda
Graduada em Matemática
Equipe Brasil Escola