Raízes de uma equação do 2º grau por soma e produto quando a ≠ 1

Nos livros didáticos não encontramos nenhuma referência sobre a obtenção das raízes de uma equação quadrática utilizando as relações de Girard quando a ≠1. De uma forma muito simples é possível obter as raízes partindo dos princípios de soma e produto. Vejamos como proceder.

Dada uma equação do segundo grau com coeficientes inteiros, ax² + bx + c = 0, com discriminante maior que zero e tal que b/a ou c/a (ou ambos) não seja um inteiro. Podemos resolver essa equação utilizando a tradicional fórmula de resolução, conhecida no Brasil como fórmula de Báskara. Tais equações também podem ser resolvidas pelo método de soma e produto.

O método de resolução por soma e produto consiste no seguinte:

Considerando a equação ax2 + bx + c =0, com a ≠ 0, suas raízes são:

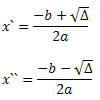
Fazendo a soma das duas raízes, obtemos:

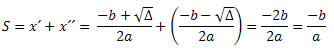
O produto das duas raízes será:

Relembrado o método, vamos analisar como determinar as raízes de uma equação do 2º grau, com a ≠ 1, utilizando soma e produto.

Sejam z₁ e z₂ dois números racionais, escritos de forma que tenham o mesmo denominador d, então:

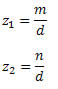
Assim, temos que:

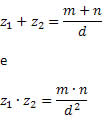
Essa informação nos dá um método de reduzir soma e produto de frações em soma e produto de inteiros.

Agora, escreva S e P como frações de forma que o denominador de P seja o quadrado do denominador de S, ou seja:

Em seguida, determine os números inteiros m e n com soma S´e produto P´. Então, m/d e n/d têm soma S e produto P.

Exemplo: Determinar as raízes da equação 12x² – 10x – 8 = 0.

Solução: Temos que

Assim, S´= 10 e P´´ = – 96, que leva a m = – 6 e n = 16. Logo, as raízes da equação são:

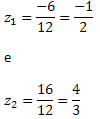
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola