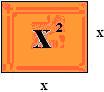PUBLICIDADE
O mulçumano al-Khowarizmi estudou a Álgebra geométrica de Euclides e resolveu uma equação do 2º grau através da mesma. O que dificulta o entendimento da linguagem utilizada por al-Khowarizmi é a falta de símbolos, por isso veja um exemplo abaixo onde uma equação do segundo grau foi resolvida utilizando a forma geométrica traduzida para a algébrica simbólica utilizada nos dias de hoje.
Dada a equação x2 + 6x = 27
• Construímos um quadrado, cuja área vai ser o termo x2.
• O termo 6x significa a área de uma retângulo, cujos lados valem 6 e x.
• Dividimos esses retângulos em quatro retângulos de mesma área.
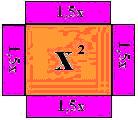
• Aplicando cada um desses quatro retângulos acima sobre os lados do quadrado de área x2, pois possui um dos lados em comum, o lado que vale x.
Agora a área formada pelo quadrado e pelos quatro retângulos será:
x2 + 4 . 1,5x = x2 + 6x.
A equação do segundo grau x2 + 6x = 27, portanto a área encontrada acima x2 + 6x será igual a 27.
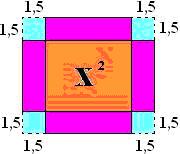
• Completando o quadrado.
Agora a área desse quadrado será a área do anterior (27) mais o que acrescentamos.
27 + 4 . (1,5 . 1,5) = 27 + 9 = 36.
Portanto, esse quadrado terá área igual a 36.
• A resolução da equação termina quando encontramos o valor de x. Então, devemos encontrar quanto vale cada lado desse quadrado. Sabemos que sua área é 36, assim seu lado irá valer o mesmo que a raiz quadrada de 36, assim teremos lado igual a 6.
√36 = 6.
• Sabendo que cada lado mede 1,5 + x + 1,5 e mede 6, formamos uma equação e descobrimos o valor de x.
1,5 + x + 1,5 = 6
3 + x = 6
x = 6 – 3
x = 3
O estudo sobre resolução de equação do 2° grau feito por al-Khowarizmi ficou quase completo o que faltou foi a aplicação dos símbolos, pois alguns cálculos matemáticos só irão ter fundamento após a introdução da Álgebra puramente simbólica.
Por Danielle de Miranda
Graduada em Matemática
Equipe Brasil Escola