PUBLICIDADE
As demonstrações de fórmulas e teoremas são fundamentais para que o aluno compreenda o pensamento matemático, os métodos e o rigor exigido, a criatividade, os erros e tentativas presentes na tarefa de demonstrar e provar a veracidade da afirmativa matemática. O que vemos, ainda hoje, é a ideia de que basta o aluno conhecer a fórmula, não é necessário saber por que a fórmula é assim. Naturalmente, essa postura não contribui em nada para fazer com que os estudantes entendam e, consequentemente, aprendam a gostar de matemática.
Vejamos uma demonstração da fórmula para sen (a + b) utilizando o teorema de Ptolomeu. Essa demonstração é perfeitamente compreensível para um aluno do ensino médio.
Partiremos da lei dos senos para um triângulo qualquer de lados a, b, c, e ângulos A, B e C, respectivamente. Temos que:
![]()
Sendo R o raio da circunferência circunscrita ao triângulo. Dessa forma, em uma circunferência de diâmetro unitário, teremos: a = sen A, b = sen B e c = sen C.
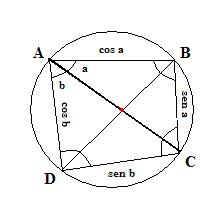
Assim, podemos interpretar o seno de um ângulo como o comprimento de uma corda definida por ele em uma circunferência de diâmetro unitário. Com essa interpretação, consideremos o quadrilátero ABCD inscrito na circunferência, como mostra a figura abaixo.
A diagonal AC é um diâmetro da circunferência. A diagonal BD equivale a sen (a + b).
O teorema de Ptolomeu afirma que, para qualquer quadrilátero inscrito em uma circunferência, tem-se o produto das diagonais igual à soma dos produtos dos lados opostos:
![]()
Da igualdade acima, obtemos:
![]()
Ou
![]()
Como queríamos demonstrar.
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola