Combinação de elementos e probabilidade
Estratégias de ensino-aprendizagem
O texto aborda a aplicação da análise combinatória no cálculo de probabilidades em jogos lotéricos, como a mega-sena. A proposta é adaptar esse contexto para o ensino de alunos do 1º e 2º ano do Ensino Médio, reduzindo o universo numérico e tornando os cálculos mais acessíveis.
Os estudos relacionados à combinação de elementos e cálculo de probabilidades são essenciais na busca do entendimento das chances de ganho dos prêmios ligados a jogos lotéricos como: mega sena, loto mania, quina entre outras. Por abranger uma grande sequência de agrupamentos de elementos, podemos adaptar esses jogos para que sejam trabalhados em sala, objetivando demonstrar ao aluno como são efetuados os cálculos desses jogos lotéricos.
É importante ressaltar que esses cálculos devem envolver alunos do 1º e 2º ano do Ensino Médio, pois estão exatamente relacionados aos assuntos envolvendo Análise Combinatória. O material a ser utilizado deve ser construído com base no existente e controlado pelas lotéricas da Caixa Econômica Federal. Para que o universo de combinações seja menor, vamos diminuir o intervalo de números e os agrupamentos de números assinalados em cada cartela.
Por exemplo, na Mega Sena temos um universo de 60 números dos quais temos que acertar 6 números para o prêmio principal, gerando simplesmente 50.063.860 combinações. Podemos reduzir o conjunto universo de elementos para 15 números, possibilitando agrupamentos de 3 números em relação ao sorteio. Dessa forma teremos 15 números agrupados 3 a 3.
Como ensinar análise combinatória em sala de aula?
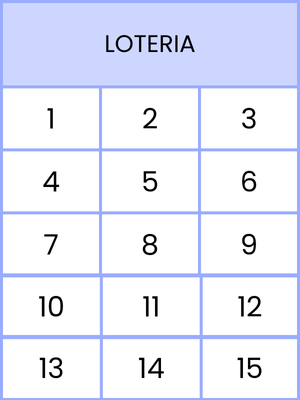
Os números que deverão ser sorteados são: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 e 15. Os agrupamentos envolvendo esses números correspondem ao total de 455 combinações. Veja algumas:
1 – 2 – 3
1 – 2 – 7
2 – 3 – 9
7 – 12 – 15
9 – 11 – 14
8 – 12 – 15
1 – 9 – 12
5 – 10 – 15
4 – 7 – 14
4 – 9 – 11
6 – 8 – 10
2 – 7 – 9
As cartelas podem ser confeccionadas ou podemos utilizar os volantes disponíveis nas lotéricas, aproveitando somente os 15 números iniciais. O sorteio dos números pode ser realizado pelo professor com o auxílio do globo de números do jogo de bingo. Nessa situação somente as pedras enumeradas de 1 a 15 deverão ser utilizadas.
O cálculo das combinações pode ser efetuado aplicando a seguinte fórmula:
\(C_{n,p} = \frac{n!}{p!(n-p)!} \)
\(C_{15,3} = \frac{15!}{3!(15-3)!} = \frac{15 \cdot 14 \cdot 13}{3 \cdot 2 \cdot 1} = 455 \)
\(C_{15,3} = 455 \)
Calcular a chance de acertos depende do número de apostas realizadas dentro dototal de 455. Por exemplo, caso uma pessoa aposte 5 cartelas, sua chance de ganhar é igual a:
\(p = \frac{5}{455} \)
\(p= 0,011\)
\( p = 1,098\% \)
As atividades apresentadas são metodologias testadas e comprovadas em relação ao aproveitamento do ensino e do aprendizado dos alunos, dessa forma o professor pode aproveitar o material divulgado ou criar mecanismos próprios a serem trabalhados.