É interessante como o uso de combinações entre apenas 10 algarismos gera todos os números conhecidos, até mesmo considerando que os números são infinitos. Os alunos precisam ter pleno conhecimento desses fatos para que as operações básicas não se refiram apenas a algorítimos – a serem utilizados sempre que for necessário somar, subtrair, multiplicar e dividir – mas a processos que eles compreendem profundamente e que fazem sentido.
Um bom ensino do sistema de numeração decimal pode desencadear o aprendizado sobre as operações básicas e seus algoritmos, que são baseadas na posição de cada algarismo, e tornar o ensino e a aprendizagem mais atraentes tanto para o professor quanto para o aluno.
Para que o ensino do sistema decimal de numeração seja efetivo, é bom que o professor considere outros sistemas de numeração como o maia ou o babilônico e discuta com seus alunos as possibilidades disponíveis para aquele sistema. Algumas dessas possibilidades estão expostas a seguir.
Proposta:
Uma proposta interessante é expor sistemas não decimais, como o babilônico (sexagesimal ou de base 60) ou o maia (vigesimal ou de base 20).
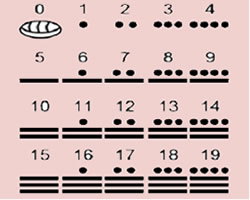
Sistema de numeração maia

Sistema de numeração babilônico
Não pare agora... Tem mais depois da publicidade ;)
Essa etapa pode ser feita por meio de explicações utilizando quadro e giz, cópias em papel ou exposição do sistema em data show (ou as três juntas se possível). É importante que os alunos compreendam o modo como os números são construídos por meio de combinações entre símbolos do sistema escolhido.
Posteriormente, proponha aos alunos que criem seus próprios sistemas numéricos. É bom que, nessa etapa, o sistema criado pelo aluno não tenha a mesma base de contagem que o sistema numérico apresentado pelo professor. Por exemplo, caso tenha discutido o sistema numérico maia (vigesimal), o professor pode propor ao aluno que crie um sistema numérico duodecimal (de base 12). Pode-se escolher um dos sistemas criados pelos alunos e propor uma segunda atividade: criar um algoritmo para a adição.
Para avaliar o progresso dos alunos, no lugar de uma prova, o professor pode escolher alguns sistemas numéricos melhor elaborados por seus alunos e dividir a classe em grupos maiores que discutirão esses sistemas numéricos. Após a discussão, proponha uma apresentação, expondo base de contagem, símbolos, e, se possível, algumas operações básicas no sistema criado por eles.
Por Luiz Paulo Moreira
Graduado em Matemática








